快速排序详细分析
注:REF[n]为参考资料,列于文章结尾。
看了编程珠玑Programming Perls第11章关于快速排序的讨论,发现自己长年用库函数,已经忘了快排怎么写。于是整理下思路和资料,把至今所了解的快排的方方面面记录与此。
纲要
- 算法描述
- 时间复杂度分析
- 具体实现细节
- 划分
- 选取枢纽元
- 固定位置
- 随机选取
- 三数取中
- 分割
- 单向扫描
- 双向扫描
- Hoare的双向扫描
- 改进的双向扫描
- 双向扫描的其他问题
- 选取枢纽元
- 分治
- 尾递归
- 划分
- 参考文献
一、算法描述(Algorithm Description)
快速排序由C.A.R.Hoare于1962年提出,算法相当简单精炼,基本策略是随机分治。
首先选取一个枢纽元(pivot),然后将数据划分成左右两部分,左边的大于(或等于)枢纽元,右边的小于(或等于枢纽元),最后递归处理左右两部分。
分治算法一般分成三个部分:分解、解决以及合并。快排是就地排序,所以就不需要合并了。只需要划分(partition)和解决(递归)两个步骤。因为划分的结果决定递归的位置,所以Partition是整个算法的核心。
对数组S排序的形式化的描述如下(REF[1]):
- 如果S中的元素个数是0或1,则返回
- 取S中任意一元素v,称之为枢纽元
- 将S-{v}(S中其余元素),划分成两个不相交的集合:S1={x∈S-{v}|x<=v} 和 S2={x∈S-{v}|x>=v}
- 返回{quicksort(S1) , v , quicksort(S2)}
二、时间复杂度分析(Time Complexity)
快速排序最佳运行时间O(nlogn),最坏运行时间O(N^2),随机化以后期望运行时间O(nlogn),关于这些任何一本算法数据结构书上都有证明,就不写在这了,一下两点很重要:
- 选取枢纽元的不同, 决定了快排算法时间复杂度的数量级;
- 划分方法的划分方法总是O(n), 所以其具体实现的不同只影响算法时间复杂度的系数。
所以诉时间复杂度的分析都是围绕枢纽元的位置展开讨论的。
三、具体实现细节(Details of Implementaion)
1、划分(Partirion)
void QuickSort(T A[], int p, int q)
{
if (p < q)
{
int q = Partition(A, p, q);
QuickSort(A, p, q-1);
QuickSort(A, q+1, r);
}
}
划分又分成两个步骤:选取枢纽元和按枢纽元将数组分成左右两部分
a.选取枢纽元(Pivot Selection)
固定位置
同样是为了方便,将选取枢纽元单独提出来成一个函数:select_pivot(T A[], int p, int q),该函数从A[p...q]中选取一个枢纽元并返回,且枢纽元放置在左端(A[p]的位置)。
int select_pivot(T A[], int p, int q)
{
return A[p];
}
但是实际应用中,数据往往是部分有序的,如果仍用两端的元素最为枢纽元,则会产生很不好的划分,使算法退化成O(n^2)。所以要采用一些手段避免这种情况,我知道的有“随机选取法”和“三数取中法”。
随机选取
int select_pivot_random(T A[], int p, int q)
{
int i = randInt(p, q);
swap(A[p], A[i]);
return A[p];
}
其中randInt(p, q)随机返回[p, q]中的一个数,C/C++里可由stdlib.h中的rand函数模拟。
三数取中
即取三个元素的中间数作为枢纽元,一般是取左端、右断和中间三个数,也可以随机选取。(REF[1])
int select_pivot_median3(T A[], int p, int q)
{
int m = (p + q)/2;
/* swap to ensure A[m] <= A[p] <= A[q] */
if (A[p] < A[m]) swap(A[p], A[m]);
if (A[q] < A[m]) swap(A[q], A[m]);
if (A[q] < A[p]) swap(A[q], A[p]);
return A[p];
}
b.按枢纽元将数组分成左右两部分
虽然说分割方法只影响算法时间复杂度的系数,但是一个好系数也是比较重要的。这也就是为什么实际应用中宁愿选择可能退化成O(n^2)的快速排序,也不用稳定的堆排序(堆排序交换次数太多,导致系数很大)。
常见的分割方法有三种:
单向扫描
int partition(T A[], int p, int q)
{
int x = select_pivot(A, p, q);
int m = p, j;
for (int j = p+1; j <= q; ++j)
/* invariant : A[p+1...m] < A[p] && A[m+1, i-1] >= x[q] */
if (A[j] <= x)
swap(A[++m], j)
swap(A[p], A[m]);
/* A[p...m-1] < A[m] <= A[m+1...u] */
return m;
顺便废话几句,在看国外的书的时候,发现老外在分析和测试算法尤其是循环时,非常重视不变量(invariant)的使用。确立一个不变量,在循环开始之前和结束之后检查这个不变量,是一个很好的保持算法正确性的手段。
事实上第一种算法需要的交换次数比较多,而且如果采用选取左端元素作为枢纽元的方法,该算法在输入数组中元素全部相同时退化成O(n^2)。第二种方法可以避免这个问题。
双向扫描
int partition(T A[], int p, int q)
{
int x = select_pivot(A, p, q);
int i = p, j = q + 1;
for ( ; ; )
{
do ++i; while (i <= q && A[i] < x);
do --j; while (A[j] > x);
if (i > j) break;
swap(A[i], A[j]);
}
swap(A[p], A[j]);
return j;
}
双向扫描可以正常处理所有元素相同的情况,而且交换次数比单向扫描要少。
Hoare的双向扫描
int partition(T A[], int p, int q)
{
int x = select_pivot(A, p, q);
int i = p - 1, j = q + 1;
for ( ; ; )
{
do --j; while (A[j] > x);
do ++i; while (A[i] < x);
if (i < j) swap(A[i], A[j])
else return j;
}
}
需要注意的是,返回值j并不是枢纽元的位置,但是仍然保证了A[p..j] <= A[j+1...q]。这种方法在效率上于双向扫描差别甚微,只是代码相对更为紧凑,并且用A[p]做哨兵元素减少了内层循环的一个if测试。
改进的双向扫描
int partition(T A[], int p, int q)
{
int x = select_pivot(A, p, q);
int i = p, j = q;
for ( ; ; )
{
while (i < j && A[j] > x) --j;
A[i] = A[j];
while (i < j && A[i] < x) ++i;
A[j] = A[i];
}
A[i] = x; // i == j
return i;
}
这种类似迭代的方法,每次只需一次赋值,减少了内存读写次数,而前面几种的方法一次交换需要三次赋值操作。由于没有哨兵元素,不得不在内层循环里判断i、j是否相交,实际上反而增加了很多内存读取操作。但是由于循环计数器往往被放在寄存器了,而如果待排数组很大,访问其元素会频繁的cache miss,所以用计数器的访问次数换取待排数组的访存是值得的。
关于双向扫描的几个问题
1.内层循环中的while测试是用“严格大于/小于”还是”大于等于/小于等于”。
一般的想法是用大于等于/小于等于,忽略与枢纽元相同的元素,这样可以减少不必要的交换,因为这些元素无论放在哪一边都是一样的。但是如果遇到所有元素都一样的情况,这种方法每次都会产生最坏的划分,也就是一边1个元素,令一边n-1个元素,使得时间复杂度变成O(N^2)。而如果用严格大于/小于,虽然两边指针每此只挪动1位,但是它们会在正中间相遇,产生一个最好的划分,时间复杂度为log(2,n)。
另一个因素是,如果将枢纽元放在数组两端,用严格大于/小于就可以将枢纽元作为一个哨兵元素,从而减少内层循环的一个测试。
由以上两点,内层循环中的while测试一般用“严格大于/小于”。
2.对于小数组特殊处理
void QuickSort(T A[], int p, int q)
{
if (q - p > cutoff) //cutoff is constant
{
int q = Partition(A, p, q);
QuickSort(A, p, q-1);
QuickSort(A, q+1, r);
}
else
InsertionSort(T A[], p, q); //user insertion sort for small arrays
}
二、分治
分治这里看起来没什么可说的,就是一枢纽元为中心,左右递归,实际上也有一些技巧。
1.尾递归(Tail recursion)
void QuickSort(T A[], int p, int q)
{
while (p < q)
{
int m = Partition(A, p, q);
QuickSort(A, p, m-1);
p = m + 1;
}
}
采用这种方法可以缩减堆栈深度,由原来的O(n)缩减为O(logn)。
三、参考文献:
- [1]Mark Allen Weiss. Data Structures and Algorithms Analysis in C++. Pearson Education, Third Edition, 2006.
- [2]Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms. MIT Press, 2001, Second Edtion, 2001.
- [3]Jon Bently. Programming Pearls. Addison Wesley, Second Edition, 2000.
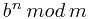 时
时 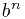 会非常大,直接去计算不是好的方法。
会非常大,直接去计算不是好的方法。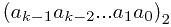
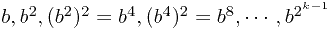
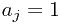 时的
时的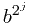 的项乘起来。
的项乘起来。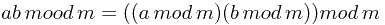
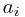 = 1 then x := (x * power) mod m
= 1 then x := (x * power) mod m